Gaussian Filter in Keras (code snippet)

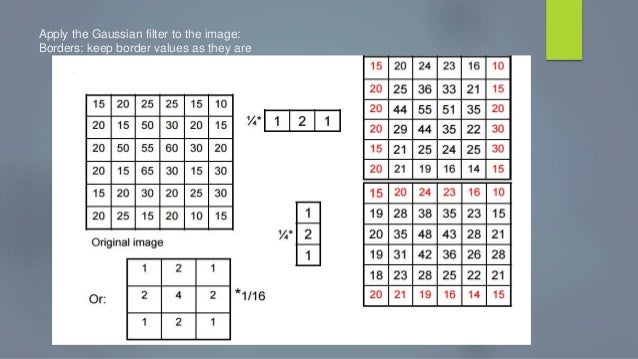
Very often we need to perform basic vision operations on a computational graph like building a Laplacian pyramid or filter a tensor with a specific precalculated filter. 

Below i present a code snippet for building a fixed non-trainable gaussian filter in keras.

import keras
import numpy as np
import scipy.stats as st

def gaussian_filter_block(input_layer,
                          kernel_size=3,
                          strides=(1, 1),
                          dilation_rate=(1, 1),
                          padding="same",
                          activation=None,
                          trainable=False,
                          use_bias=False):
    """
    Build a gaussian filter block
    :return:
    """

    def _gaussian_kernel(kernlen=[21, 21], nsig=[3, 3]):
        """
        Returns a 2D Gaussian kernel array
        """
        assert len(nsig) == 2
        assert len(kernlen) == 2
        kern1d = []
        for i in range(2):
            interval = (2 * nsig[i] + 1.) / (kernlen[i])
            x = np.linspace(-nsig[i] - interval / 2., nsig[i] + interval / 2.,
                            kernlen[i] + 1)
            kern1d.append(np.diff(st.norm.cdf(x)))

        kernel_raw = np.sqrt(np.outer(kern1d[0], kern1d[1]))
        # divide by sum so they all add up to 1
        kernel = kernel_raw / kernel_raw.sum()
        return kernel

    # Initialise to set kernel to required value
    def kernel_init(shape, dtype):
        kernel = np.zeros(shape)
        kernel[:, :, 0, 0] = _gaussian_kernel([shape[0], shape[1]])
        return kernel

    return keras.layers.DepthwiseConv2D(
        kernel_size=kernel_size,
        strides=strides,
        padding=padding,
        depth_multiplier=1,
        dilation_rate=dilation_rate,
        activation=activation,
        use_bias=use_bias,
        trainable=trainable,
        depthwise_initializer=kernel_init,
        kernel_initializer=kernel_init)(input_layer)

from my open source project https://github.com/NikolasMarkou/multiscale_variational_autoencoder

Gaussian 2d

I needed to compute a 2-dimensional Gaussian distribution which is very common when using Gabor filters.
First google result Custom 2D Gauss  provided a quick solution but upon first look the implementation didn't take advantage of any of matlab's features (i.e matrix manipulation) or included functions so it is a bit slow.

I ended rigging it up a bit making it very fast.

One problem I didn't address is adding a scale for the pixels but that can be fixed inside applications by scaling the standard deviation.

The code in Matlab:

function mat = Gaussian2d(...
    gsize, center, sigmax, sigmay, theta, offset, factor)
% GAUSSIAN2d - Produces a 2-dimensional gaussian matrix
%
%   Input
%   gsize   :  Size of the output 'gauss', should be a 1x2 vector
%   center  :  The center position of the gaussian [row col]
%   sigmax  :  Std. dev. in the X direction
%   sigmay  :  Std. dev. in the Y direction
%   theta   :  Rotation in degrees
%   offset  :  Minimum value in output
%   factor  :  Related to maximum value of output, should be 
%                    different from zero  
%
%   Output
%   mat     : probability vector for each angle bin 
%-------------------------------------------------------------------------
%%  Validate input arguments
    if ~exist('gsize','var')
        error('Error : gsize argument not set');
    end
    
    if ~exist('center','var')
        center = gsize / 2;
    end
    
    if ~exist('sigmax','var')
        sigmax = 1;
    end
    
    if ~exist('sigmay','var')
        sigmay = 1;
    end
    
    if ~exist('theta','var')
        theta = 0;
    end
     
    if ~exist('offset','var')
        offset = 0;
    end
    
    if ~exist('factor','var')
        factor = 1;
    end
    theta  = (theta/180)*pi;  
%-------------------------------------------------------------------------
%%  Compute
    [X,Y] = meshgrid(1:gsize(1),1:gsize(2));
    Xc  = X - center(1);
    Yc  = Y - center(2);
    xm  = (Xc)*cos(theta) - (Yc)*sin(theta);
    ym  = (Xc)*sin(theta) + (Yc)*cos(theta);
    u   = (xm / sigmax).^2 + (ym / sigmay).^2;
    mat = offset + factor * exp(-u/2);
end

The code in C# in the OpenCv framework :

        /// Create a rotated 2d Gaussian distribution 
        /// </summary>
        /// <param name="_width">Width of the result image in pixels</param>
        /// <param name="_height">Height of the result image in pixels</param>
        /// <param name="_centerX">X-coordinate of the center of the distribution in pixels</param>
        /// <param name="_centerY">Y-coordinate of the center of the distribution in pixels</param>
        /// <param name="_sigmaX">Standard deviation of X-axis in pixels</param>
        /// <param name="_sigmaY">Standard deviation of Y-axis in pixels</param>
        /// <param name="_theta">Rotation of the distribution in degrees</param>
        /// <param name="_offset">Resulting value offset</param>
        /// <param name="_factor">Resulting value multiplier</param>
        /// <returns></returns>
        public static Image<Gray, float> Gaussian2D(
            int   _width    = 10, 
            int   _height   = 10,
            float _centerX  = 5, 
            float _centerY  = 5,
            float _sigmaX   = 1.0f, 
            float _sigmaY   = 1.0f,
            float _theta    = 0.0f, 
            float _offset   = 0.0f, 
            float _factor   = 1.0f)
        {
            float[, ,] data = new float[_height, _width, 1];
            float xc, yc, xm, ym , tmpX, tmpY, u,
                cosTheta = (float)Math.Cos(_theta / 180.0f * Math.PI), 
                sinTheta = (float)Math.Sin(_theta / 180.0f * Math.PI);
            _sigmaX = 1.0f / _sigmaX;
            _sigmaY = 1.0f / _sigmaY;
            for (int i = 0; i < _width; i++)
            {
                xc = i - _centerX;
                for (int j = 0; j < _height; j++)
                {
                    yc = j - _centerY;
                    xm = xc * cosTheta - yc * sinTheta;
                    ym = xc * sinTheta + yc * cosTheta;
                    tmpX = xm * _sigmaX;
                    tmpY = ym * _sigmaY;
                    u = tmpX * tmpX + tmpY * tmpY;
                    data[j, i, 0] = _offset + _factor * (float)Math.Exp(-u / 2);
                }
            }
            return new Image<Gray,float>(data);
        }